1.论文概要

研究背景：

✡︎论文链接。由于高光谱图像（HSI）本生的高维度和“噪声”导致常规的CNN不能较好的利用高光谱图像的空谱特征，加之随着CNN层数的增加效果反而更差。为了解决以上困扰本文提出深度金字塔（Pyramidal）网用于高光谱图像分类。有别于一般的残差网，Pyramidal残差网类似于金字塔形状逐渐增加卷积层特征图的维度，在网络更深层次涉及更多的特征，同时平衡每层的时间复杂度.同时，应对HSI高复杂性的创新研究线之一是更好的挖掘空间-光谱特征的结合，它的实现比单纯的像素分类效果更好，此类方法通过将每个像素的光谱与其所属的相应结构的尺寸和形状相结合来使分类不确定性降低。

算法改进：

常规残差网络（ResNet）通过残差块来改进CNN，促进更深层网络的学习并使网络层次更深入。本文通过基于金字塔瓶颈残差块建立网络，使用光谱信息和空间信息来实现快速准确的高光谱分类。与金字塔形似，越接近输出的网络层特征学习图越大。便于学习更多的有价值特征。同时网络对训练样本数量也要求较少。

实验验证：

基于四个常见的高光谱数据集，与10种不同的高光谱图像分类算法对比，在精度和时间复杂度上本文算法都很有竞争力。

2.算法应用

网络架构基础

采用2D-CNN,但是所有波段都将用于输入数据，为了保留原始光谱特征不采用类似PCA的降维方法。CNN层中包括卷积层、Batch normalization层(减少协方差偏移，在每批特征图上强加高斯分布)、Nonlinearity层(学习非线性表示)和池化层。

残差单元的改进

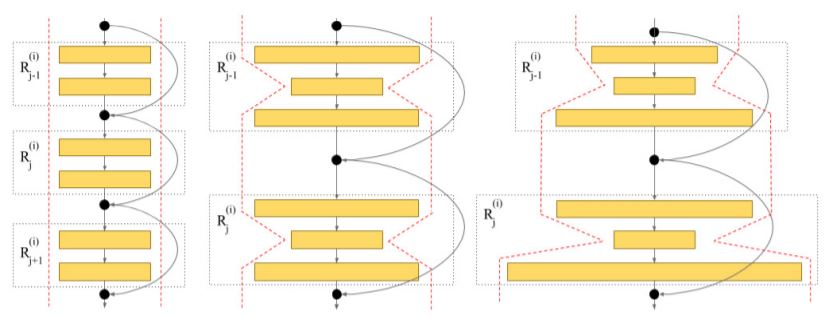
如图1，从左到右分别给出了传统残差块、瓶颈残差块和金字塔瓶颈残差块。传统残差块从上到下具有相同的拓扑，瓶颈残差块中的特征图先被缩小然后恢复输入时的大小，这样的结构有助于残差单元更快的执行。最后金字塔残差块单元中，CONV层的通道数逐渐增加，导致各层逐渐变宽。随之带来一个问题，残差块中最终的原始输入特征映射$p_j$(通过跳跃连接而来)与残差函数$F(p_j,w_j)$的结果之间的维度不同，本文采用 [1] 中零填充快捷方式，即添加额外的零条目直到达到增加的维度。

网络设计

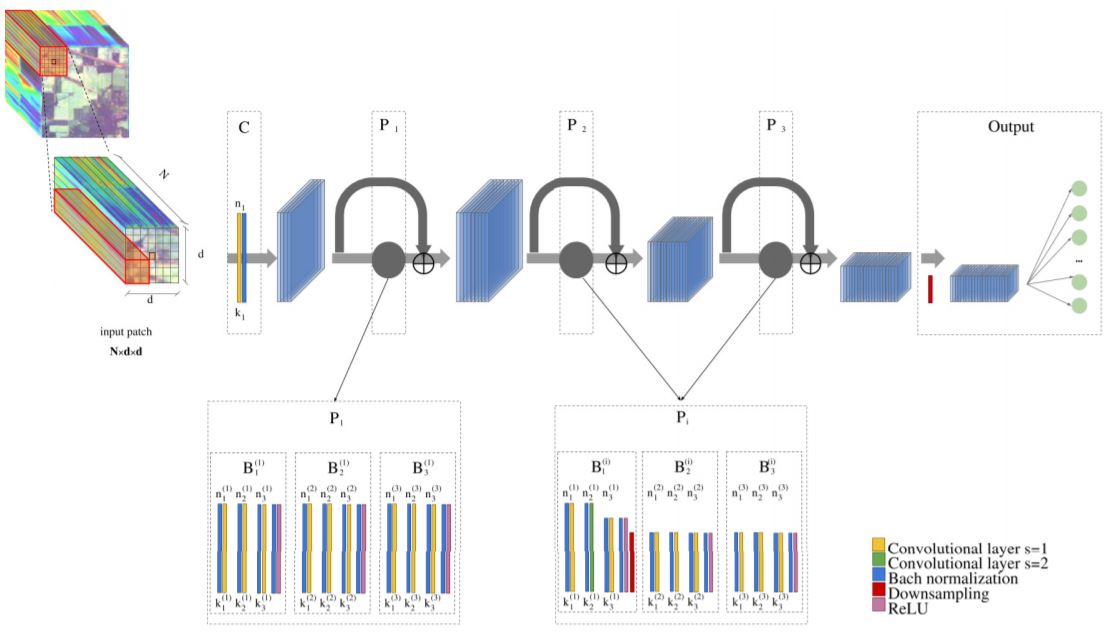
图2给出了模型体系结构，右下角标记出了各个颜色代表的不同功能层。其中$C$为输入模块，$P_1-P_3$被命名为金字塔残差模块，里面包含若干金字塔瓶颈残差单元$B$。Patch单位的数据依次通过如图的五个模块，组成了很深的网络。
图中每个$B^{(i)}_j$由几类层堆叠而成。三个Conv层前面分别有Bach normalization层在单元的末端加入Relu激活层。实现了每个Conv层考虑了其输入特征中所有的光谱信息，同时处理了窗口内的空间信息。在$P_2$和$P_3$中加入了由平均池化层构成的下采样层，来减少数据方差并从空间邻域中提取低级别的特征来提供给下一层。在网络设计中采用 [1] 中的方法线性地增加每个残差单元的特征图深度。具体每层滤波器属性取值在原文表1列出。学习率的设置，在前150epochs中设置为0.1，后50epochs设为0.01。

3.实验

对比实验包含10中不同的分类方法，分别为：1) SVM with radial basis function kernel [2]; 2) RF; 3) MLP;4) extreme learning machine (ELM) [3]; 5) kernel ELM(KELM) [4]; 6) 1-D CNN; 7) 2-D CNN; 8) 3-D-CNN;9) spectral–spatial ResNet (SSRN) [5]; 10) deep fast CNN (DFCNN)

实验内容包括四个不同的实验，用于验证相对于标准分类器(SVM,RF,MLP,2D-CNN,3D-CNN)的性能（实验1），不同的训练数据百分比比较（实验2），与最近的两个基于CNN的空谱分类器进行比较（实验3和4）。其中实验二特别在IP和UP数据集，遵循相同配置，尺寸大小为N×7×7，分别使用5％，10％，15％，20％和25％的训练比比较。实验三与SSRN的比较中采用四种不同的空间大小5×5,7×7,9×9,11×11，在IP和KSC数据集中用20%作为训练数据，UP数据集中用10%作为训练数据。实验四与DFCNN比较时采用9×9,15×15,19×19三种空间尺寸大小。

实验1结果显示本文算法较其他标准分类器不仅在精度上有所提升，而且用时较短。实验2结果显示在IP数据集中当训练样本达到20%各算法分类精度提升变缓慢，而在UP数据集中同样的效果只需5%。同时在相同训练样本比下，本文算法在分类精度上表现最好。在与同样是根据空谱信息结合进行分类的算法对比中，本文算法在相同输入空间尺寸下，不仅精度有所提高，而且标准差较其他两个方法小。

☛参考文献

[1] D. Han, J. Kim, and J. Kim, “Deep pyramidal residual networks,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jul. 2017,pp. 6307–6315, doi: 10.1109/CVPR.2017.668
[2] B. Waske, S. van der Linden, J. Benediktsson, A. Rabe, and P. Hostert,“Sensitivity of support vector machines to random feature selection in classification of hyperspectral data,” IEEE Trans. Geosci. Remote Sens.,vol. 48, no. 7, pp. 2880–2889, Jul. 2010.
[3] G.-B. Huang, H. Zhou, X. Ding, and R. Zhang, “Extreme learning machine for regression and multiclass classification,”IEEE Trans.Syst.,Man, Cybern. B, Cybern., vol. 42, no. 2, pp. 513–529, Apr. 2012.
[4] G.-B. Huang and C.-K. Siew, “Extreme learning machine with randomly assigned RBF kernels,” Int. J. Inf.Technol., vol. 11, no. 1, pp. 16–24,2005.
[5] Z. Zhong, J. Li, Z. Luo, and M. Chapman, “Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework,” IEEE Trans. Geosci. Remote Sens., vol. 56, no. 2,pp. 847–858, Feb. 2018.